6.1 急弯处溃坝流(Dam-break Flow through Sharp Bend)
待研究的物理模型由上游近似正方形的水库与一条 L 形渠道组成。水库区以及 L 形渠道两段交汇转角处的流动基本为二维;然而数值与实验均表明,在两段直线渠道中流动主要呈一维特征。溃坝流中两类特征尤为关注:
• 转角的“阻尼效应(damping effect)”
• 在转角处形成的向上游传播的水跃(hydraulic jump)
此外,水库内膨胀波(expansion wave)的多次反射也为检验数值模型二维能力提供了机会。由于水库内流动将保持为亚临界(subcritical)且波幅较小,可据此检查计算中是否存在过度数值耗散(excessive numerical dissipation)。
6.1.1 物理试验(Physical experiments)
Frazão 与 Zech(2002、1999a、1999b)报道了关于 90° 转弯渠道溃坝流的系统性实验研究。渠道由两段直线段构成:长度分别为 3.92 m 与 2.92 m,宽度均为 0.495 m;两段直线段以直角连接,并通过一个 $0.495\times0.495\,\mathrm{m}$ 的方形单元实现转角过渡。渠道纵坡为 0。L 形渠道通过一扇断头闸门(guillotine-type gate)与一个尺寸约为 $2.44\times2.39\,\mathrm{m}$ 的近方形水库相连。水库底高程比渠道底床低 33 cm。下游边界设置溜槽(chute)。详细布置见附图。
Frazão 与 Zech 分别在干床(dry bed)与湿床(wet bed)条件下进行了测量。本文对比采用的情形为:水库初始静止,初始自由水面高出渠道底床 20 cm,即水库初始水深为 53 cm;渠道底床初始为干。通过稳态流试验评估得到的 Manning 系数分别为:底床 0.0095、渠道壁 0.0195,单位为 $\mathrm{s/m^{1/3}}$。
水位在 6 个测点进行测量。测点位置见图 6.1,坐标列于表 6.1。
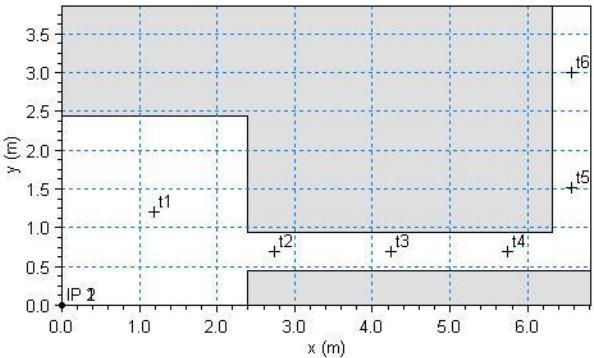
图 6.1 Frazão 与 Zech(2002)试验布置
表 6.1 水位测点位置
| 位置 | $x(m)$ | $y(m)$ |
| $T1$ | $1.19$ | $1.20$ |
| $T2$ | $2.74$ | $0.69$ |
| $T3$ | $4.24$ | $0.69$ |
| $T4$ | $5.74$ | $0.69$ |
| $T5$ | $6.56$ | $1.51$ |
| $T6$ | $6.56$ | $3.01$ |
6.1.2 数值试验(Numerical experiments)
数值模拟同时采用二维与三维浅水方程。
使用非结构网格,共 18311 个三角形单元与 9537 个节点。最小边长 0.01906 m,最大边长 0.06125 m。三维模拟中垂向离散采用 10 层。时间步长为 0.002 s。下游边界采用自由出流(吸收型,absorbing)边界条件。湿润水深(wetting depth)、淹没阈值(flooding depth)与干涸阈值(drying depth)分别为 0.002 m、0.001 m 与 0.0001 m。
二维模拟采用常量 Manning 系数 $105.26\,\mathrm{m^{1/3}/s}$;三维模拟采用常量糙率高度 $5\cdot10^{-5}\,\mathrm{m}$。
6.1.3 结果(Results)
图 6.2 给出了 6 个测点处计算水面高程(surface elevations)的时间序列,并与实测值对比。图 6.3 给出二维模拟在 $T=1.6\,\mathrm{s}$、$3.2\,\mathrm{s}$ 与 $4.8\,\mathrm{s}$ 时刻的水面高程等值线图。
图 6.4 给出了在 $T=6.4\,\mathrm{s}$ 时刻,沿中心线一条垂向剖面(从 $(x,y)=(5.7,0.69)$ 到 $(x,y)=(6.4,0.69)$)处的流速矢量图与等值线图。
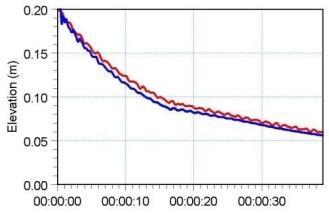
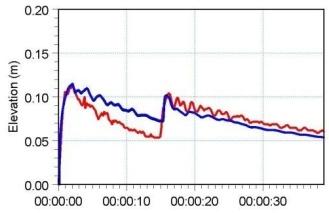
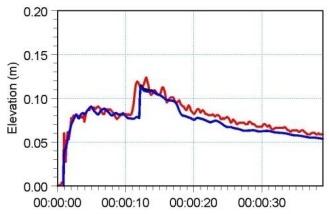
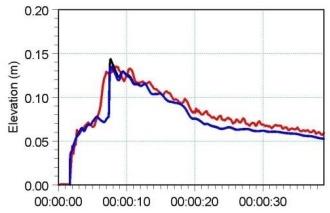
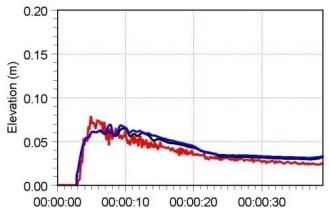
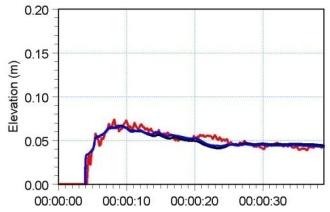
图 6.2 六个测点处水位随时间演化。(蓝色)3D 计算,(黑色)2D 计算,(红色)Frazão 与 Zech(1999a,b)实测
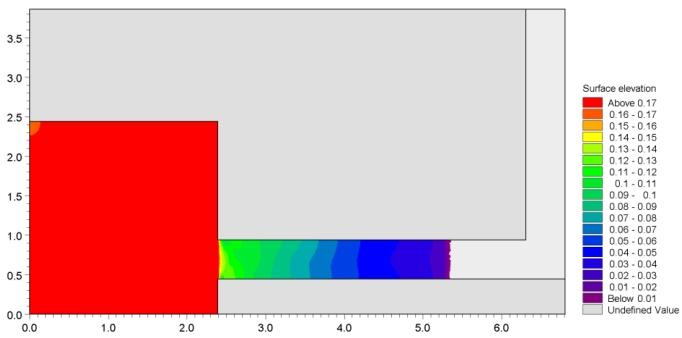
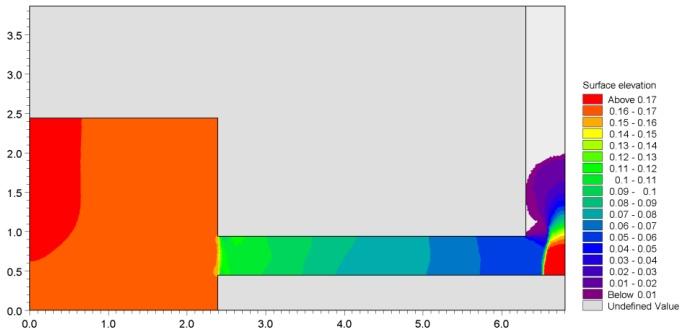
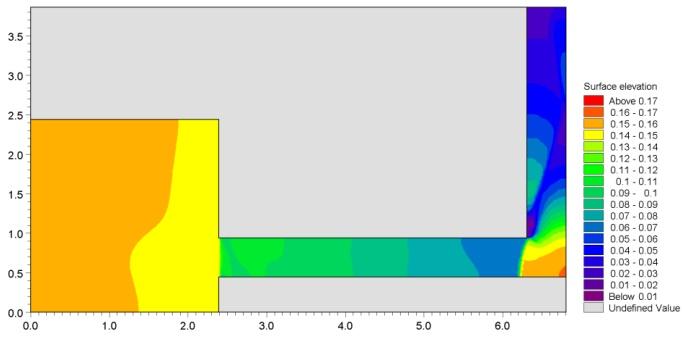
图 6.3 水面高程等值线图:$T=1.6\,\mathrm{s}$(上)、$T=3.2\,\mathrm{s}$(中)、$T=4.8\,\mathrm{s}$(下)
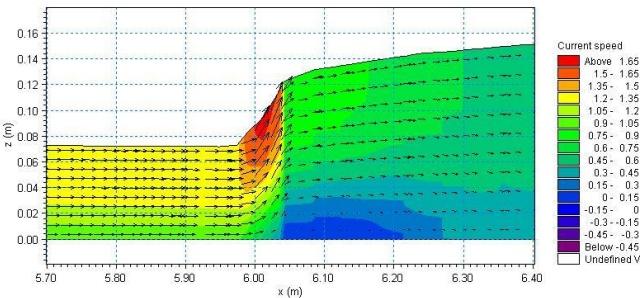
图 6.4 $T=6.4\,\mathrm{s}$ 时沿中心线垂向剖面的流速矢量图与等值线图
