3.1 空间离散
求解域内的离散采用有限体积法(finite volume method)。空间域通过将连续体划分为互不重叠的单元/网格单元(cells/elements)来离散。
在二维情况下,单元可以为任意形状多边形,但本文仅考虑三角形与四边形单元。
在三维情况下采用分层网格(layered mesh):水平面使用非结构网格(unstructured mesh),垂向使用结构网格(structured mesh)(见图 3.1)。垂向网格可基于 $\sigma$ 坐标,或采用 $\sigma/z$-层混合坐标。对于混合 $\sigma/z$ 网格,自由表面至指定深度采用 $\sigma$ 坐标,而其下采用 $z$-层坐标。不同类型的垂向网格示意见图 3.2。$\sigma$ 域与 $z$-层域内的单元可以为三棱柱或四棱柱(底面为三边形或四边形多边形),因此水平面单元为三角形或四边形。单元在垂向上严格对齐(perfectly vertical),且各层具有相同的拓扑结构(identical topology)。
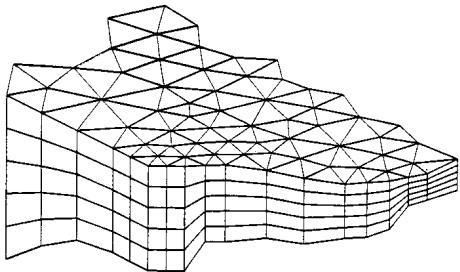
图 3.1 三维情形的网格剖分原理
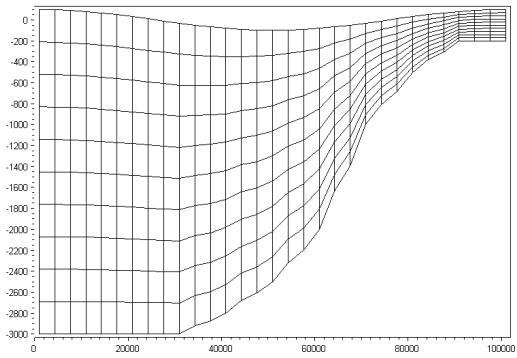
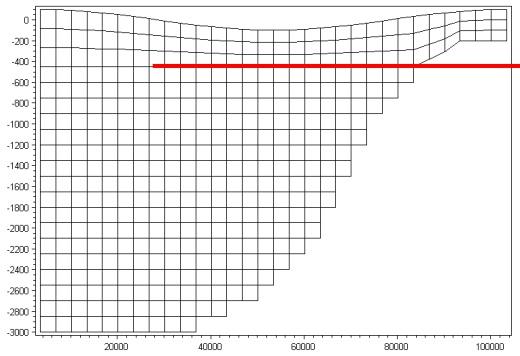
图 3.2 不同垂向网格示意。上:$\sigma$ 网格;下:带简单地形调整(bathymetry adjustment)的 $\sigma/z$ 混合网格。红线表示 $z$-层域与 $\sigma$-层域的分界面。
使用 $\sigma$ 坐标的最重要优点在于:能够精确表征地形(bathymetry),并在近底部提供一致的分辨率。然而,在地形突变(陡坡)区域,$\sigma$ 坐标可能在水平压力梯度、平流与混合项中产生显著误差,从而导致不真实的流场。
使用 $z$-层坐标可使水平压力梯度、平流与混合项的计算更为直接,但其缺点是地形表达精度不足;同时,由于地形呈“台阶状”表达(stair-step representation),可能在近底部产生不真实的流速。
3.1.1 垂向网格(Vertical Mesh)
垂向离散可采用标准 $\sigma$ 网格或 $\sigma/z$-层混合网格。对于混合 $\sigma/z$ 网格,自由表面至指定深度 $z_{\sigma}$ 采用 $\sigma$ 坐标,其下采用 $z$-层坐标。为允许自由表面高程变化,至少需要一个 $\sigma$ 层。
(1)$\sigma$ 网格
在 $\sigma$ 域内使用固定层数 $N_{\sigma}$,每一层厚度为 $\sigma$ 域总厚度 $h_{\sigma}$ 的固定比例,其中 $h_{\sigma}=\eta-\max(z_{b},z_{\sigma})$。$\sigma$ 域离散由一组离散的 $\sigma$ 层面 $\{\sigma_{i},\,i=1,(N_{\sigma}+1)\}$ 给出。这里 $\sigma$ 从最低 $\sigma$ 层底界面的 $\sigma_{1}=0$ 变化到自由表面的 $\sigma_{N_{\sigma}+1}=1$。
可变 $\sigma$ 坐标可采用 Song and Haidvogel (1994) 提出的通用垂向坐标($s$-coordinate)系统的离散形式构造。首先在 $s$ 坐标系($-1\le s\le 0$)上定义等距离散:
$$ s_{i}=-\frac{N_{\sigma}+1-i}{N_{\sigma}}\qquad i=1,(N_{\sigma}+1)\tag{3.1} $$
然后由下式得到离散 $\sigma$ 坐标:
$$ \sigma_{i}=1+\sigma_{c}s_{i}+\big(1-\sigma_{c}\big)c\big(s_{i}\big)\quad i=1,(N_{\sigma}+1)\tag{3.2} $$
其中:
$$ c(s)=(1-b)\frac{\sinh(\theta s)}{\sinh(\theta)}+b\frac{\tanh\left(\theta\left(s+\frac{1}{2}\right)\right)-\tanh\left(\frac{\theta}{2}\right)}{2\tanh\left(\frac{\theta}{2}\right)}\tag{3.3} $$
这里 $\sigma_c$ 为等距分布与拉伸分布之间的权重系数,$\theta$ 为表层控制参数,$b$ 为底层控制参数。权重系数范围为 $0<\sigma_{c}\le1$:$\sigma_c=1$ 对应等距分布,$\sigma_c=0$ 对应完全拉伸分布;$\sigma_c$ 过小可能导致线性不稳定。表层控制参数范围为 $0<\theta\le20$,底层控制参数范围为 $0\le b\le1$。当 $\theta<1$ 且 $b=0$ 时可得到等距垂向分辨率;增大 $\theta$ 可使表层附近分辨率最高;当 $\theta>0$ 且 $b=1$ 时,表层与底层附近均可获得较高分辨率。
可变垂向离散的网格示例见图 3.3 与图 3.4。
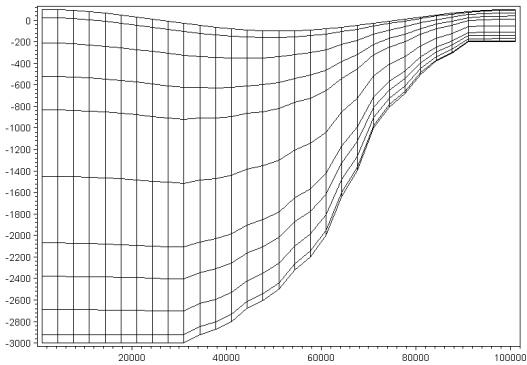
图 3.3 基于层厚分配的垂向分布示例。层数:10;第 1–10 层厚度:0.025、0.075、0.1、0.01、0.02、0.02、0.1、0.1、0.075、0.025
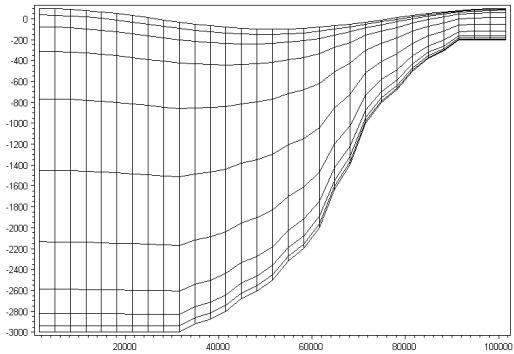
图 3.4 基于可变分布的垂向分布示例。层数:10,$\sigma_{c}=0.1$,$\theta=5$,$b=1$
(2)$\sigma/z$-层混合网格(Combined sigma/z-level)
在 $z$-层域内,离散由一组离散的 $z$ 层面 $\{z_{i},\,i=1,(N_{z}+1)\}$ 给出,其中 $N_z$ 为 $z$-层域内的层数。$z_1$ 为最小 $z$ 层面,$z_{N_z+1}$ 为最大 $z$ 层面,且等于 $\sigma$ 深度 $z_{\sigma}$。相应层厚为:
$$ \Delta z_{i}=z_{i+1}-z_{i}\qquad i=1,N_{z}\tag{3.4} $$
离散示意见图 3.5 与图 3.6。
采用标准 $z$-层离散时,底深会被“舍入”到最接近的 $z$ 层面。因此,对水平网格中的某单元,其单元平均底深为 $z_b$,当满足以下条件时,该单元在 $z$ 域对应柱状网格中的层单元被纳入计算:
$$ \frac{(z_{i+1}-z_{i})}{2}\ge z_{b}\quad i=1,N_{z}\tag{3.5} $$
单元平均底深 $z_b$ 取该单元各顶点(vortices)处水深的平均值。对标准 $z$-层离散,最小深度为 $z_1$。为在底深低于最小 $z$ 层面($z_{1}>z_{b}$)时仍能反映真实水深,采用贴底(bottom fitted)修正:在底层单元引入层厚修正系数 $f_1$,用于体积与面通量积分计算。底层修正系数为:
$$ f_{1}=\frac{(z_{2}-z_{b})}{\Delta z_{1}}\tag{3.6} $$
修正后的底层层厚为 $\Delta z_{1}^{*}=f_{1}\Delta z_{1}$。简单地形调整方法见图 3.5。
为更精确表达底深,可采用高级(advanced)地形调整方法。对单元平均底深为 $z_b$ 的水平网格单元,当满足以下条件时,其 $z$ 域柱状网格中的层单元被纳入计算:
$$ z_{i+1}>z_{b}\quad i=1,N_{z}\tag{3.7} $$
并对层厚引入修正系数 $f_i$:
$$ f_{i}=\max\left(\frac{(z_{i+1}-z_{b})}{\Delta z_{i}},\frac{\Delta z_{min}}{\Delta z_{i}}\right)\quad z_{i}<z_{b}<z_{i+1}\ \text{or}\ z_{1}>z_{b}\tag{3.8} $$
$$ f_{i}=1\quad z_{1}\ge z_{b} $$
其中 $\Delta z_{min}$ 为最小层厚阈值,用于避免修正系数过小。修正系数用于体积与面通量积分计算;修正后的层厚为 $\{\Delta z_{i}^{*}=f_{i}\Delta z_{i},\,i=1,N_{z}\}$。高级地形调整方法见图 3.6。
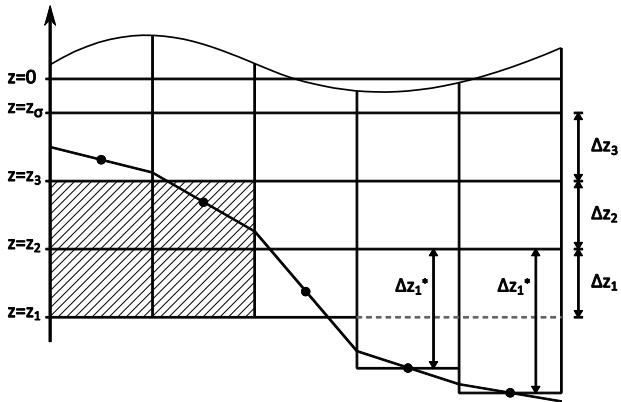
图 3.5 简单地形调整方法
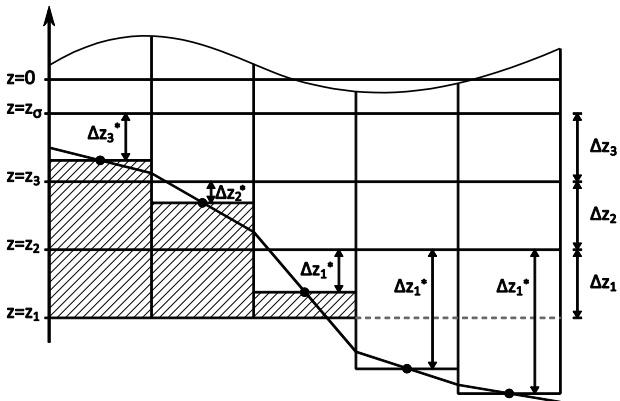
图 3.6 高级地形调整方法
3.1.2 浅水方程(Shallow water equations)
浅水方程组的积分形式可写为一般守恒律形式:
$$ \frac{\partial\boldsymbol{U}}{\partial t}+\nabla\cdot\boldsymbol{F}\big(\boldsymbol{U}\big)=\boldsymbol{S}\big(\boldsymbol{U}\big)\tag{3.9} $$
其中:$\boldsymbol{U}$ 为守恒变量向量,$\boldsymbol{F}$ 为通量向量函数,$\boldsymbol{S}$ 为源项向量。
在笛卡尔坐标下,二维浅水方程组可写为:
$$ \frac{\partial\boldsymbol{U}}{\partial t}+\frac{\partial\left(\boldsymbol{F}_{x}^{I}-\boldsymbol{F}_{x}^{V}\right)}{\partial x}+\frac{\partial\left(\boldsymbol{F}_{y}^{I}-\boldsymbol{F}_{y}^{V}\right)}{\partial y}=\boldsymbol{S}\tag{3.10} $$
其中上标 $I$ 与 $V$ 分别表示无黏(对流)通量与黏性通量,并且:
$$ \boldsymbol{U}=\left[\begin{aligned}h\\ h\overline{u}\\ h\overline{v}\end{aligned}\right]\tag{3.11a} $$
$$ \boldsymbol{F}_{x}^{I}=\left[\begin{aligned}h\overline{u}\\ h\overline{u}^{2}+\frac{1}{2}g(h^{2}-d^{2})\\ h\overline{u}\,\overline{v}\end{aligned}\right],\quad\boldsymbol{F}_{x}^{V}=\left[\begin{aligned}0\\ hA\left(2\frac{\partial\overline{u}}{\partial x}\right)\\ hA\left(\frac{\partial\overline{u}}{\partial y}+\frac{\partial\overline{v}}{\partial x}\right)\end{aligned}\right]\tag{3.11b} $$
$$ \boldsymbol{F}_{y}^{I}=\left[\begin{aligned}h\overline{v}\\ h\overline{u}\,\overline{v}\\ h\overline{v}^{2}+\frac{1}{2}g(h^{2}-d^{2})\end{aligned}\right],\quad\boldsymbol{F}_{y}^{V}=\left[\begin{aligned}0\\ hA\left(\frac{\partial\overline{u}}{\partial y}+\frac{\partial\overline{v}}{\partial x}\right)\\ hA\left(2\frac{\partial\overline{v}}{\partial y}\right)\end{aligned}\right]\tag{3.11c} $$
$$ \boldsymbol{S}=\left[\begin{aligned}0\\ g\eta\frac{\partial d}{\partial x}+f\overline{v}h-\frac{h}{\rho_{0}}\frac{\partial p_{a}}{\partial x}-\frac{gh^{2}}{2\rho_{0}}\frac{\partial\rho}{\partial x}-\frac{1}{\rho_{0}}\left(\frac{\partial s_{xx}}{\partial x}+\frac{\partial s_{xy}}{\partial y}\right)+\frac{\tau_{sx}}{\rho_{0}}-\frac{\tau_{bx}}{\rho_{0}}+hu_{s}\\ g\eta\frac{\partial d}{\partial y}-f\overline{u}h-\frac{h}{\rho_{0}}\frac{\partial p_{a}}{\partial y}-\frac{gh^{2}}{2\rho_{0}}\frac{\partial\rho}{\partial y}-\frac{1}{\rho_{0}}\left(\frac{\partial s_{yx}}{\partial x}+\frac{\partial s_{yy}}{\partial y}\right)+\frac{\tau_{sy}}{\rho_{0}}-\frac{\tau_{by}}{\rho_{0}}+hv_{s}\end{aligned}\right]\tag{3.11d} $$
在笛卡尔坐标下,三维浅水方程(在 $\sigma$ 坐标下的三维动量-连续方程通量形式)可写为:
$$ \frac{\partial\boldsymbol{U}}{\partial t}+\frac{\partial\boldsymbol{F}_{x}^{I}}{\partial x^{\prime}}+\frac{\partial\boldsymbol{F}_{y}^{I}}{\partial y^{\prime}}+\frac{\partial\boldsymbol{F}_{\sigma}^{I}}{\partial\sigma}+\frac{\partial\boldsymbol{F}_{x}^{V}}{\partial x}+\frac{\partial\boldsymbol{F}_{y}^{V}}{\partial y}+\frac{\partial\boldsymbol{F}_{\sigma}^{V}}{\partial\sigma}=\boldsymbol{S}\tag{3.12} $$
其中上标 $I$ 与 $V$ 分别表示无黏(对流)与黏性通量,并且:
$$ \boldsymbol{U}=\left[\begin{aligned}h\\ hu\\ hv\end{aligned}\right]\tag{3.13a} $$
$$ \boldsymbol{F}_{x}^{I}=\left[\begin{aligned}hu\\ hu^{2}+\frac{1}{2}g(h^{2}-d^{2})\\ huv\end{aligned}\right],\quad\boldsymbol{F}_{x}^{V}=\left[\begin{aligned}0\\ hA\left(2\frac{\partial u}{\partial x}\right)\\ hA\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\end{aligned}\right]\tag{3.13b} $$
$$ \boldsymbol{F}_{y}^{I}=\left[\begin{aligned}hv\\ huv\\ hv^{2}+\frac{1}{2}g(h^{2}-d^{2})\end{aligned}\right],\quad\boldsymbol{F}_{y}^{V}=\left[\begin{aligned}0\\ hA\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\\ hA\left(2\frac{\partial v}{\partial y}\right)\end{aligned}\right]\tag{3.13c} $$
$$ \boldsymbol{F}_{\sigma}^{I}=\left[\begin{aligned}h\omega\\ h\omega u\\ h\omega v\end{aligned}\right],\quad\boldsymbol{F}_{\sigma}^{V}=\left[\begin{aligned}0\\ \frac{\nu_{t}}{h}\frac{\partial u}{\partial\sigma}\\ \frac{\nu_{t}}{h}\frac{\partial v}{\partial\sigma}\end{aligned}\right]\tag{3.13d} $$
$$ \boldsymbol{S}=\left[\begin{aligned}0\\ g\eta\frac{\partial d}{\partial x}+fvh-\frac{h}{\rho_{0}}\frac{\partial p_{a}}{\partial x^{\prime}}-\frac{hg}{\rho_{0}}\int_{z}^{\eta}\frac{\partial\rho}{\partial x}\,dz-\frac{1}{\rho_{0}}\left(\frac{\partial s_{xx}}{\partial x}+\frac{\partial s_{xy}}{\partial y}\right)+hu_{s}\\ g\eta\frac{\partial d}{\partial y}-fuh-\frac{h}{\rho_{0}}\frac{\partial p_{a}}{\partial y^{\prime}}-\frac{hg}{\rho_{0}}\int_{z}^{\eta}\frac{\partial\rho}{\partial y}\,dz-\frac{1}{\rho_{0}}\left(\frac{\partial s_{yx}}{\partial x}+\frac{\partial s_{yy}}{\partial y}\right)+hv_{s}\end{aligned}\right]\tag{3.13e} $$
将式 (3.9) 在第 $i$ 个单元上积分,并用 Gauss 定理将通量体积分改写为边界积分,得:
$$ \int_{A_{i}}\frac{\partial\boldsymbol{U}}{\partial t}\,d\Omega+\int_{\Gamma_{i}}\left(\boldsymbol{F}\cdot\boldsymbol{n}\right)\,ds=\int_{A_{i}}\boldsymbol{S}\big(\boldsymbol{U}\big)\,d\Omega\tag{3.14} $$
其中:$A_i$ 为第 $i$ 个单元的面积/体积;$\Omega$ 为定义在 $A_i$ 上的积分变量;$\Gamma_i$ 为第 $i$ 个单元边界;$ds$ 为沿边界的积分变量;$\boldsymbol{n}$ 为边界上的外法向单位向量。
对面积/体积积分采用一点求积(取单元几何中心为求积点),对边界积分采用中点求积,则式 (3.14) 可写为:
$$ \frac{\partial \boldsymbol{U}_{i}}{\partial t}+\frac{1}{A_{i}}\sum_{j=1}^{N_{S}}\left(\boldsymbol{F}\cdot\boldsymbol{n}_{j}\right)\Delta\Gamma_{j}=\boldsymbol{S}_{i}\tag{3.15} $$
其中:$\boldsymbol{U}_i$ 与 $\boldsymbol{S}_i$ 分别为第 $i$ 个单元内的 $\boldsymbol{U}$ 与 $\boldsymbol{S}$ 的平均值,存储在单元中心;$N_S$ 为单元边数;$\boldsymbol{n}_j$ 为第 $j$ 条边界面的外法向单位向量;$\Delta\Gamma_j$ 为第 $j$ 条界面的长度/面积。
空间离散可采用一阶或二阶格式。
对二维情形,在单元界面处的对流通量采用近似 Riemann 求解器(Roe 格式,Roe, 1981)计算。Roe 格式需要估计界面左右两侧的状态变量。为实现二阶空间精度,采用线性梯度重构(linear gradient-reconstruction)。平均梯度按 Jawahar and Kamath (2000) 的方法估计。为避免数值振荡,使用二阶 TVD 斜率限制器(Van Leer limiter,见 Hirch, 1990;Darwish, 2003)。
对三维情形,在单元的垂直界面($x'y'$ 平面)对流通量同样采用 Roe 近似 Riemann 求解器,并采用线性梯度重构与 Van Leer TVD 限制器以获得二阶空间精度。水平界面(沿垂向方向的界面)上的对流通量:低阶格式使用一阶迎风(first order upwinding);高阶格式则用界面上下相邻单元计算得到通量的均值来近似。
3.1.3 输运方程(Transport equations)
输运方程出现在盐温模型、湍流模型与通用输运模型中,均具有笛卡尔坐标下式 (2.20) 的形式。二维情况下,输运方程的积分形式可用式 (3.9) 表示,其中:
$$ \boldsymbol{U}=h\overline{C}\tag{3.16a} $$
$$ \boldsymbol{F}^{I}=\left[h\overline{u}\,\overline{C},\ h\overline{v}\,\overline{C}\right],\quad\boldsymbol{F}^{V}=\left[hD_{h}\frac{\partial\overline{C}}{\partial x},\ hD_{h}\frac{\partial\overline{C}}{\partial y}\right]\tag{3.16b} $$
$$ \boldsymbol{S}=-hk_{p}\overline{C}+hC_{s}S\tag{3.16c} $$
三维情况下,输运方程的积分形式同样可用式 (3.9) 表示,其中:
$$ \boldsymbol{U}=hC\tag{3.17a} $$
$$ \boldsymbol{F}^{I}=\left[huC,\ hvC,\ h\omega C\right],\quad\boldsymbol{F}^{V}=\left[hD_{h}\frac{\partial C}{\partial x},\ hD_{h}\frac{\partial C}{\partial y},\ h\frac{D_{v}}{h}\frac{\partial C}{\partial\sigma}\right]\tag{3.17b} $$
$$ \boldsymbol{S}=-hk_{p}C+hC_{s}S\tag{3.17c} $$
输运方程的有限体积离散形式同样由式 (3.15) 给出。与浅水方程类似,空间离散可采用一阶或二阶格式。
在二维中,低阶格式使用简单的一阶迎风:迎风侧单元平均值作为边界值;高阶格式通过梯度重构在边界得到二阶精度,并采用迎风侧取值。为增强稳定性并抑制振荡,使用 TVD-MUSCL 限制器(见 Hirch, 1990;Darwish, 2003)。
在三维中,低阶格式同样使用一阶迎风;高阶格式在水平边界上通过近似水平梯度获得二阶精度,仍取迎风侧值。为稳定并减少振荡,采用 ENO(Essentially Non-Oscillatory)型程序限制水平梯度;在垂向方向采用三阶 ENO 程序以获得垂向面通量所需的面值(Shu, 1997)。
