5.1 近场计算(Nearfield Calculations)
近场解基于 Jirka (2004) 所述的积分喷流模型方程,通过在给定环境条件下求解体积通量与动量通量、盐度与温度(若包含)等守恒方程,确定喷流/羽流的稳态解。
假设速度剖面以及状态参数与标量质量的分布满足高斯(Gaussian)形式。喷流模型采用夹带(entrainment)闭合方法,将横向剪切与方位向剪切(azimuthal shear)机制对夹带的贡献区分开来;并包含一个二次定律的湍流阻力机制($F_{D}$),该机制由近期关于横向喷流入横向来流(transverse jets into crossflow)动力学的实验研究所建议。依据 Jirka (2004) 的体积(连续方程)、全局方向动量分量、状态参数与标量质量守恒,可得到:
$$ \frac{dQ}{ds}=E \tag{5.1} $$
$$ \frac{dM_{x}}{ds}=Eu_{a}+F_{D}\sqrt{1-\cos^{2}\theta\cos^{2}\sigma} \tag{5.2} $$
$$ \frac{dM_{y}}{ds}=-F_{D}\frac{\cos^{2}\theta\sin\sigma\cos\sigma}{\sqrt{1-\cos^{2}\theta\cos^{2}\sigma}} \tag{5.3} $$
$$ \frac{dM_{z}}{ds}=\pi\lambda^{2}b^{2}g_{c}^{\prime}-F_{D}\frac{\sin\theta\cos\theta\cos\sigma}{\sqrt{1-\cos^{2}\theta\cos^{2}\sigma}} \tag{5.4} $$
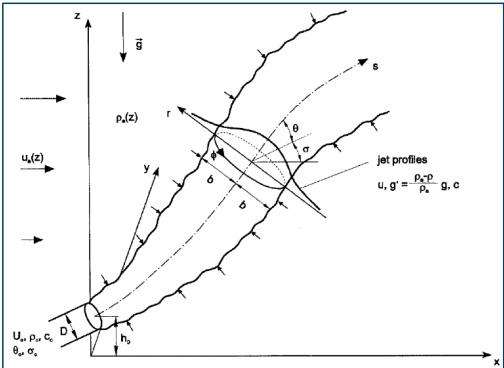
图 5.1 近场喷流积分模型定义示意图
其中 $s$ 为沿喷流轨迹的轴向距离,$E$ 为夹带率;$b$ 为喷流特征宽度(定义为喷流半径,使喷流超额速度为 $e^{-1}=37\%$ 时对应的半径)。中心线密度包含在中心线浮力加速度 $g_{c}^{\prime}$ 的定义中,并由 UNESCO 状态方程按盐度 $S$ 与温度 $T$ 计算:
$$ \rho_{Jet}=\rho_{UNESCO}(S,T) \tag{5.5} $$
若喷流中含有泥沙且其动力学被纳入计算,则喷流密度会按泥沙存在进行修正(可通过在 MT 模块中定义源并激活 MT-HD 反馈实现):
$$ \rho_{Jet}=(1-C_{sed})\rho_{Jet}+C_{sed}\rho_{sed} \tag{5.6} $$
其中 $C_{sed}$ 为体积分数泥沙浓度(由用户在 MT 模块中为 Jet 源提供的泥沙浓度换算得到),$\rho_{sed}$ 为泥沙密度(由用户在 MT 模块 MT-HD 反馈中提供)。随后定义浮力加速度($\rho_{a}$ 为环境密度,$\rho_{ref}$ 为参考密度,由 HD 模块中用户提供的参考盐度与温度计算):
$$ g_{c}^{\prime}=\frac{\rho_{Jet}-\rho_{a}}{\rho_{ref}}g \tag{5.7} $$
影响喷流轨迹与稀释率的两个关键物理过程是夹带率 $E$ 与环境阻力 $F_{D}$。夹带率与喷流中心线速度的顺流向贡献 $u_{c}$ 以及环境速度横向分量的方位向贡献 $u_{a}\sqrt{1-\cos^{2}\theta\cos^{2}\sigma}$ 成正比:
$$ E=2\pi bu_{c}\left(\alpha_{1}+\alpha_{2}\frac{\sin\theta}{F_{l}^{2}}+\alpha_{3}\frac{u_{a}\cos\theta\cos\sigma}{u_{c}+u_{a}}\right)+2\pi bu_{a}\sqrt{1-\cos^{2}\theta\cos^{2}\sigma}\,\alpha_{4}\left|\cos\theta\cos\sigma\right| \tag{5.8} $$
其中 $F_{l}$ 为局部密度弗劳德数(local densimetric Froude number):
$$ F_{l}=\frac{u_{c}}{\sqrt{g_{c}^{\prime}b}} \tag{5.9} $$
夹带函数中顺流向部分的第一项代表“纯喷流(pure jet)”效应,第二项加入“纯羽流(pure plume)”效应,第三项对应“纯尾迹(pure wake)”。Jirka (2004) 建议的经验系数为:
$$ \alpha_{1}=0.055,\quad\alpha_{2}=0.6,\quad\alpha_{3}=0.055,\quad\alpha_{4}=0.5 \tag{5.10} $$
喷流偏折源于横向来流对其施加的压差阻力($F_{D}$)以及喷流夹带横向运动流体所产生的动量贡献($Eu_{a}$)。阻力以二次定律参数化(Jirka, 2004):
$$ F_{D}=\frac{1}{2}C_{D}\,2\sqrt{2}\,b\,u_{a}^{2}\left(1-\cos^{2}\theta\cos^{2}\sigma\right) \tag{5.11} $$
喷流直径计算为 $2\sqrt{2}b$,$C_{D}$ 为阻力系数,按 Chan et al. (1976) 作为喷流与环境速度比的函数。
喷流轨迹计算沿轨迹增量距离 $ds$ 离散。根据 Lee and Cheung (1990) 的建议:
$$ ds=dt\left(u_{c}+u_{a}\cos\theta\cos\sigma\right) \tag{5.12} $$
其中:
$$ dt=\frac{0.1D}{u_{c}} $$
且将 $dt$ 截断限制在 0.001 s 与 1.0 s 之间,$D$ 为初始喷流直径。
近场模型在每个 HD 时间步内计算喷流轨迹与稀释,直至到达近场区末端。尽管 HD 时间步可能远小于喷流到达近场末端所需时间,但假设背景流(环境)随时间的变化尺度慢于喷流从排放点到远场释放点的传播时间。
