5.3 近场—远场耦合(Nearfield-Farfield model coupling)
近场与远场耦合包括两部分:读取环境条件作为近场喷流模型输入,以及在近场结束时将喷流排放释放到远场水动力模型。
环境流条件可取喷流位置处的局地条件,或取上游环境条件(upstream ambient)。上游选项可用于避免在释放物质受环境平流主导时,喷流解与环境流之间产生不真实反馈。对上游环境条件,在上游流向距离喷流位置一定距离处取值,该距离为:由网格确定的特征长度与用户指定最小上游距离二者的较大值。此处特征长度定义为初始释放点处局地单元面积平方根的 2.3 倍。
在近场区末端(由上一节任一条件确定),最终(已稀释)喷流排放在对应空间点释放到远场模型,确保在正确位置释放正确体积与稀释度。排放被分配为多个源点,覆盖与最终喷流直径对应的平面区域,并对体积与其他标量采用高斯分布;源点数量取决于远场模型网格分辨率。
由于夹带作用,近场末端的喷流流量增大,该增大量在每个水动力时间步注入远场模型,并在下一步影响水动力解。远场模型所解的浅水方程在处理此类相对较大体积的注入与加速时可能出现不充分表现(与局地网格与水深有关),导致流场不够真实。作为部分补救,在每个释放源点处向动量方程加入沿喷流释放方向的强迫(动量通量):
$$ F_{x}=M\cos\theta\cos\sigma,\quad F_{y}=M\cos\theta\sin\sigma \tag{5.13} $$
近场末端增大的排放量及其稀释度来自沿轨迹的夹带。远场模型的质量与体积守恒要求移除在释放点注入的这部分“超额质量与体积”。为此,引入沿喷流中心线轨迹分布的夹带汇(entrainment sinks)(见图 5.3),汇点数量取决于远场网格分辨率。该方法遵循 Choi and Lee (2007) 提出的分布式夹带汇方法(Distributed Entrainment Sink Approach, DESA)。
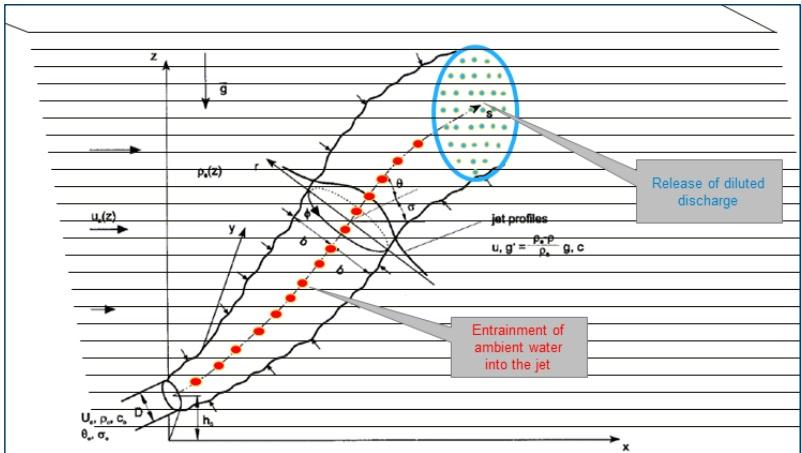
图 5.3 三维域中沿轨迹布置夹带汇的位置以及在释放位置处的分布式源点示意
与释放点类似,在汇点处从域内扣除体积也可能在汇点附近产生可疑的流场(与网格分辨率有关)。因此,沿用释放点的处理逻辑:在每个汇点处向动量平衡加入一个与环境流速度方向相反的强迫(动量通量),其大小为汇率与环境流速度的乘积。该处理对汇点诱导的垂向速度影响有限,因此在垂向喷流中更为显著。
$$ f_{x}=-q_{sink}u_{a,x} \tag{5.14a} $$
$$ f_{y}=-q_{sink}u_{a,y} \tag{5.14b} $$
