3.1 空间离散
- 结构网格(structured grids)(图3.2):每个网格点(顶点、节点)由索引$i,j,k$唯一标识,对应的笛卡尔坐标分别为$x_{i,j,k}$、$\gamma_{i,j,k}$ 与 $z_{i,j,k}$。二维单元为四边形,三维单元为六面体。若网格如图3.1a所示为贴体网格,则也称为曲线坐标网格(curvilinear grid)。
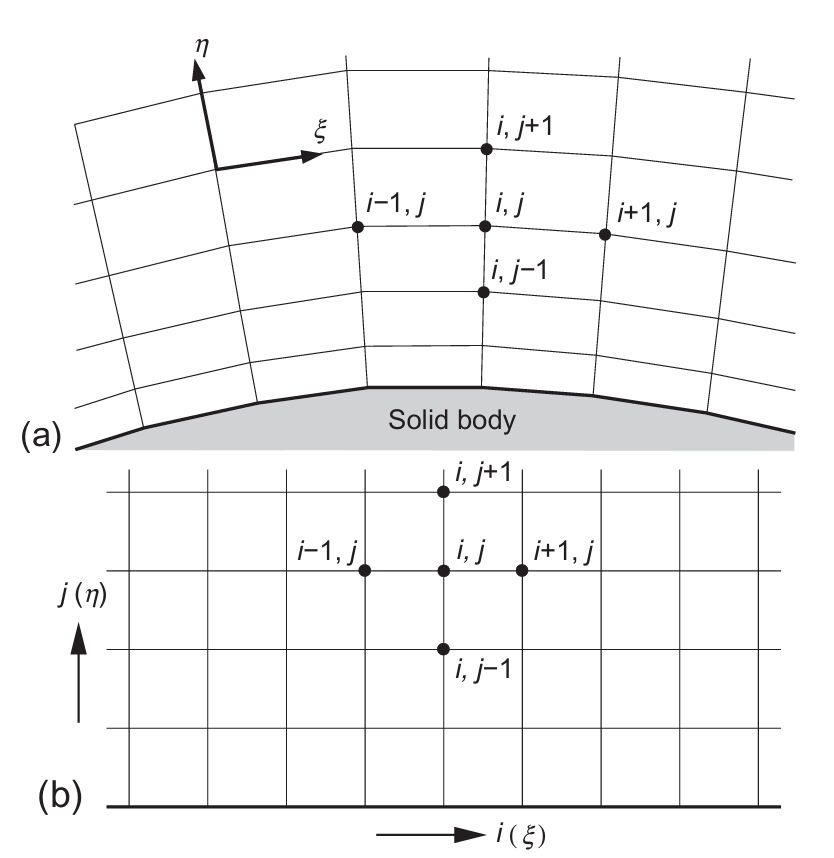 图3.2 结构化贴体的网格方法(2D):(a)展示了物理空间;(b)展示了计算空间;ξ和η表示曲线坐标系
图3.2 结构化贴体的网格方法(2D):(a)展示了物理空间;(b)展示了计算空间;ξ和η表示曲线坐标系
- 非结构网格(unstructured grids)(图3.3):单元与网格点没有特定顺序,即无法仅凭索引直接识别邻近单元或节点(例如“单元6与单元119相邻”)。过去二维多为三角形、三维多为四面体;现在为准确分辨边界层,非结构网格通常在二维由四边形与三角形混合构成,在三维由六面体、四面体、棱柱体与金字塔单元混合构成,因此称为混合网格(hybrid or mixed grids)。
结构网格的主要优点来自其索引$i,j,k$构成线性地址空间——也称计算空间(computational space),因为它直接对应流动变量在计算机内存中的存储方式。该特性使得访问某节点邻居非常快捷:只需对相应索引加减整数(例如$(i+1)$、$(k-3)$等——见图3.2)。因此梯度、通量的计算以及边界条件的处理都大幅简化。隐式格式的实现也更容易,因为通量Jacobian矩阵有良好的有序带状结构。但其缺点也很明显:对复杂几何,生成结构网格很困难。如图3.4所示,一种办法是将物理空间划分为若干拓扑更简单的部分——块(blocks),每个块更易于网格化,因此称为多块方法(multiblock approach)$[32–36]$。当然,流动求解器会更复杂,因为需要特殊逻辑在块间交换物理量或通量。若允许界面两侧网格点独立布置,即不要求网格线在块边界严格对齐(如图3.4中C或F内部所示),则可获得更强灵活性。位于块界面仅一侧的网格点称为悬挂节点(hanging nodes)。该方法的优势很直观:每个块的网格线数量可按需独立选择;其代价是对悬挂节点进行守恒处理需要更高的开销$[37,38]$。多块方法也为并行计算中的区域分解提供了有趣可能性。然而,即便如此,对复杂构型的网格生成往往仍需较长时间(常为数周或数月)。
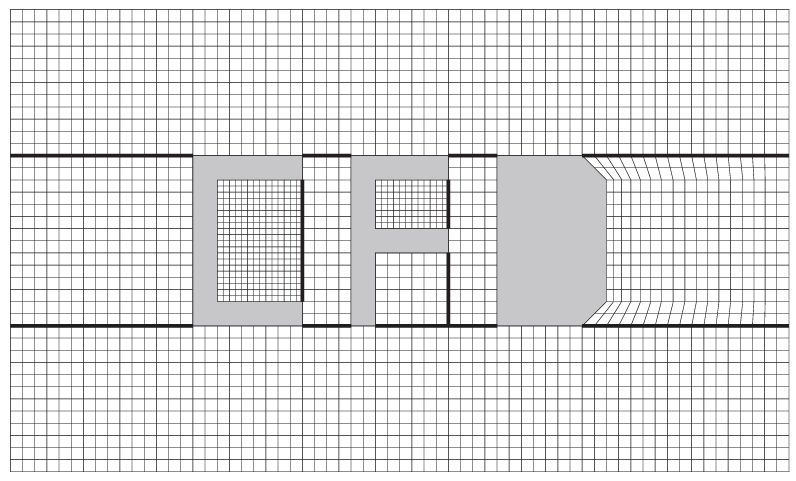 图3.4 具有符合/不符合块间接口的结构化多块网格;粗线表示块边界。
图3.4 具有符合/不符合块间接口的结构化多块网格;粗线表示块边界。
与块结构网格相关的另一种方法是Chimera技术$[39–46]$。其基本思想是:先分别在域内每个几何实体周围独立生成网格,然后将这些网格组合,使它们在交界处相互重叠。图3.5给出了简单构型的示意。关键操作是在重叠区域内在不同网格间准确传递物理量,因此重叠范围会根据所需插值阶数进行调整。相较于多块方法,Chimera的优点在于:各网格可完全独立生成,无需显式处理网格界面;其问题在于:控制方程的守恒性质在重叠区域内无法严格满足。将该方法扩展到非结构网格的研究见文献$^{[47,48]}$。
第二类网格是非结构网格。它们在处理复杂几何方面提供最大灵活性$[49]$。其主要优点在于:二维三角网格或三维四面体网格原则上可自动生成,与域的复杂性无关。当然在实践中仍需恰当设置参数以获得高质量网格。此外,为准确分辨边界层,通常建议在二维近壁使用矩形单元、在三维近壁使用棱柱体或六面体单元$[50–60]$。混合网格的另一个好处是减少网格单元、边、面以及可能的网格点数量。但也应注意:对几何要求很高的情况,混合网格生成并不简单。尽管如此,为复杂构型生成非结构混合网格所需时间通常仍显著少于多块结构网格。随着仿真几何保真度快速提高,快速且尽量少用户干预地生成网格变得愈发重要,工业环境尤甚。非结构网格的进一步优势是:基于解的网格加密与粗化可以相对自然、无缝地处理。非结构方法的缺点之一是:求解器内需要更复杂的数据结构,这类结构通常使用间接寻址,视硬件而定会降低计算效率;同时内存需求通常也高于结构格式。但尽管存在这些困难,短周转时间内处理复杂几何的能力仍更为重要。因此,例如几乎所有商业CFD软件供应商都已转向非结构求解器并不令人意外。关于非结构网格上空间与时间离散方法的综述见文献$[61]$。
生成网格之后,下一个问题是如何离散控制方程。正如前述,基本可在有限差分、有限体积与有限元三种方法间选择。下面分别简要讨论。
3.1.1 有限差分法
有限差分法是最早用于求解微分方程的数值方法之一,最早可能由Euler在1768年使用。有限差分法直接作用于控制方程的微分形式,其基本原理是利用Taylor级数展开来离散流动变量的导数。为说明,考虑如下例子:
假设我们要在某一点$x_{0}$处计算标量函数$U(x)$的一阶导数。将$U(x_{0}+\Delta x)$按$x$作Taylor展开,有
$$U(x_{0}+\Delta x)=U(x_{0})+\Delta x\frac{\partial U}{\partial x}\Big|_{x_{0}}+\frac{\Delta x^{2}}{2}\frac{\partial^{2}U}{\partial x^{2}}\Big|_{x_{0}}+\cdots.\tag{3.1}$$
由此可得对$U$一阶导数的近似
$$\frac{\partial U}{\partial x}\bigg|_{x_{0}}=\frac{U(x_{0}+\Delta x)-U(x_{0})}{\Delta x}+\mathcal{O}(\Delta x).\tag{3.2}$$
上述近似为一阶精度,因为截断误差(记作$\mathcal{O}(\Delta x)$)与余项中最大项同阶,并随$\Delta x$的一次幂趋于零(关于精度阶的讨论见Chapter 10)。同样程序可用于推导更高精度的有限差分公式以及更高阶导数的近似。
有限差分法的重要优点是简单;另一个优点是容易得到高阶逼近,从而获得空间离散的高阶精度。另一方面,由于该方法要求结构网格,其应用范围明显受限。此外,有限差分法不能直接在贴体(曲线坐标)中使用,必须先将控制方程变换到笛卡尔坐标系——换言之,从物理空间变换到计算空间(图3.2)。问题在于:坐标变换Jacobian会出现在流动方程中(见例如A.1节),该Jacobian必须一致离散以避免引入额外数值误差$[62]$。因此,有限差分法仅能直接用于较简单几何。如今它主要用于湍流研究,以及结合浸入边界单元(图3.1b)用于生物学问题。更多细节可参见例如$[63]$或偏微分方程数值解的相关教材。
3.1.2 有限体积法
控制体相对于网格的形状与位置有多种定义方式,其中两种基本方法是:
- 单元中心(cell-centered)格式(图3.6a):流动量存储于网格单元质心,控制体与网格单元一致。
- 单元顶点(cell-vertex)格式(图3.6b):流动量存储于网格点。此时控制体可以是共享该网格点的所有单元的并集,或以该网格点为中心的某个体积。前一种称为重叠控制体(overlapping control volumes),后一种称为对偶控制体(dual control volumes)。
我们将在空间离散的两章(第4章与第5章)中讨论cell-centered与cell-vertex表述的利弊。
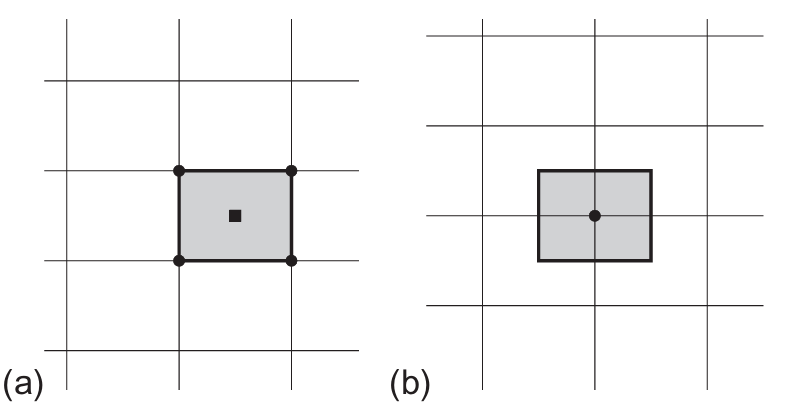 图3.6单元中心(a)和单元顶点(双控制体积)方案(b)的控制体积。
图3.6单元中心(a)和单元顶点(双控制体积)方案(b)的控制体积。
有限体积法的主要优点是:空间离散直接在物理空间中完成,因此不像有限差分法那样存在物理/计算坐标变换问题。与有限差分法相比,有限体积法还更灵活:可较容易地在结构网格与非结构网格上实现,使其特别适合模拟复杂几何内/外流动。
由于有限体积法基于守恒律的直接离散,数值格式也能守恒质量、动量与能量。这带来另一个重要特性:能够正确计算控制方程的弱解(weak solutions)。不过在Euler方程情形下还需满足一条额外条件——熵条件(entropy condition),因为弱解并不唯一。熵条件可防止出现违反热力学第二定律(熵降低)的非物理解,如膨胀激波。守恒离散的进一步结果是:解的不连续(如激波或接触间断)处必须满足的Rankine-Hugoniot关系可以被直接满足。
有趣的是,在某些条件下,可证明有限体积法等价于有限差分法,或等价于低阶有限元方法。由于这些吸引人的性质,有限体积法如今非常流行并被广泛使用。后续章节将详细介绍该方法。
3.1.3 有限元法
有限元法最初仅用于结构分析,由Turner等人于1956年首次提出$^{[65]}$。约10年后,研究者开始将有限元法用于连续介质中的场方程数值解。但直到20世纪90年代初,有限元法才在Euler与Navier-Stokes方程的求解中逐渐流行。经典有限元方法的良好入门可参见$^{[66]}$,其在流动问题中的应用见$^{[67-70]}$。近些年研究重点转向一种称为间断Galerkin(discontinuous Galerkin)格式的变体$[71-98]$,其高阶表述特别适用于气动声学应用。
在有限元方法中,需要将控制方程由微分形式变换为等价的积分形式,可通过两种不同方式实现:第一种基于变分原理,即寻找某个泛函取极值的物理解;第二种称为加权残值法或弱形式(weak formulation),要求残差的加权平均在整个物理域上恒为零。残差可视为近似误差。弱形式与有限体积守恒离散具有相同优点——可处理激波等不连续,因此弱形式通常优于变分方法。间断Galerkin格式与经典有限元的区别在于其质量矩阵(mass matrix)被定义为局部于生成单元,这使其可以使用简单显式方法在时间上推进未知系数。
有限元法因其积分表述与非结构网格而具有吸引力,二者都适合复杂几何的流动问题。除气动声学外,该方法也特别适合处理非Newton流体。有限元法具有严谨的数学基础,尤其对椭圆与抛物问题。尽管在某些情况下可证明其与有限体积离散数学等价,但数值代价明显更高,这可能解释了为何有限体积法在标准流动问题中更受欢迎。不过两者有时会结合使用——尤其在非结构网格上。例如边界处理与粘性通量离散常常“借用”有限元方法的做法。
3.1.4 其他离散方法
还有少数数值方法在某些情形下优于上述方法,这里简要提及三种代表性方法。
谱元法
谱元法(spectral-element method)$[99–107]$ 结合了有限元技术的几何灵活性与谱方法的高阶空间精度(例如10阶)及快速收敛性$[101]$。该方法基于对解的高阶多项式表示(通常为Lagrange插值),并结合标准Galerkin有限元或加权残值法。谱元法适用于解具有高阶正则性的特定问题,或高阶正则性并非例外的情形,例如不可压缩流体力学,特别适合涡流。其优点主要在于对对流算子的近似具有低耗散、低色散特性,并且对对流-扩散边界层的逼近良好。若满足高阶正则性条件,该方法可处理几何与物理都复杂的问题。除应用范围相对较窄外,其主要缺点是:与有限体积等方法相比数值代价非常高。
格子Boltzmann方法
格子Boltzmann方法(LBM)在20世纪90年代末作为格子气体方法的继任者提出,随着强大的大规模并行计算系统日益可用而变得流行$[108–129]$。与前述基于宏观守恒量(质量、动量、能量)的传统方法不同,LBM将流体建模为由虚拟粒子构成。粒子在离散格点网格上反复执行微观传播与碰撞过程。该方法基于动理学理论,可视为连续Boltzmann方程的一种特殊离散形式。一般而言,LBM在局部计算碰撞效应并将其视为弛豫过程(碰撞步),然后将结果——离散分布函数——沿特征方向发送到相邻点(传播步)。宏观场则通过对分布函数取离散矩得到,压力场也可直接由密度分布得到。需要指出的是,基于Chapman-Enskog理论,可以从LBM算法恢复连续方程与Navier-Stokes方程。近年的研究还展示了LBM与有限差分法之间的有趣相似性,并比较了两者的计算效率$[123]$。
由于其粒子动力学与局部更新特性,LBM在复杂边界或包含微观相互作用时相较传统CFD具备优势。例如,多相/多组分流动由于界面运动与变形而极具挑战,尤其是相间过渡边界。LBM通过修改碰撞算子,为处理此类问题提供相对简单且一致的途径;相分离可由粒子动力学自动产生,无需额外操控界面。因此,LBM已成功用于界面不稳定性、气泡/液滴动力学、固体表面润湿、液滴电流体动力变形等模拟,也用于多孔介质多相流、气动声学或微流控等领域。
“碰撞-传播”算法使LBM非常适合用区域分解进行高效并行处理。另一方面,传统LBM本质上是时间推进方法(物理时间或伪时间),收敛到目标(可能为定常)解的速度相对较慢。此外,目前尚无能够处理强可压缩效应流动的LBM表述,因此跨声速或超声速流动无法用LBM模拟。
无网格方法
另一种近年来引起一定兴趣的离散方法是无网格方法(gridless method)$[130-136]$。该方法空间离散仅使用点云(clouds of points),不要求像传统结构/非结构方法那样将点连接成网格。无网格方法基于控制方程在笛卡尔坐标系下的微分形式,通过最小二乘重构使用特定数量的邻点来确定流动变量梯度。由于不需要坐标变换、面面积或体积计算,它既不是有限差分、有限体积也不是有限元方法,可视为有限差分与有限元的混合。其主要优点是:像非结构方法一样具有处理复杂构型的灵活性,并且可以按需放置或聚集点(点云)。例如在计算梯度时,可以更容易地仅选取沿特征方向的邻点。然而仍有一个未解决问题:虽然无网格方法求解的是Euler或Navier-Stokes方程的守恒形式,但质量、动量与能量是否真正得到保证尚不十分明确。
无论选择何种空间离散方法,必须确保格式是一致的(consistent),即当网格充分加密时,数值解应收敛到离散方程的解。因此必须检查网格加密(例如网格点数加倍)时解的变化幅度;若解只发生很小变化,则称为网格收敛解(grid converged solution)。另一个显而易见的要求是:离散格式的精度阶应与所求解的流动问题相匹配。该规则有时会因追求更快收敛而被放弃,尤其在工业环境中(“差的解也好过没有解”)。这当然非常危险。我们将在Chapter 10再次回到精度、稳定性与一致性的问题。
3.1.5 中心与迎风格式
到目前为止,我们只讨论了空间离散的基本选择。但在上述三类方法——有限差分、有限体积与有限元——内部,还存在多种用于空间离散的具体数值格式。在此背景下,将对流通量与粘性通量的离散区分开来是很方便的,即分别处理式(2.19)中的$\langle\vec{F}_{mathrmc}\rangle$与$\vec{F}_{v}$。由于粘性通量的物理性质,合理的做法只能是用中心差分(中心平均)进行离散。因此在结构网格上离散粘性通量很直接;在非结构三角/四面体网格上,即便采用有限体积格式,粘性通量也最好用Galerkin有限元方法近似$[137]$。对于非结构混合网格情况更复杂,需要对梯度作修正平均更为合适$[138–142]$。
真正的多样性体现在对流通量的离散上。为分类方便,下面将注意力限制在为有限体积法开发的格式上,尽管大多数概念也可直接用于有限差分或有限元法。
中心格式
第一类是完全基于中心差分或中心平均的格式,称为中心格式(central schemes)。其原理是在控制体某一侧面上,通过对左右两侧的守恒变量作平均来评估通量。由于中心格式无法识别并抑制解的奇偶解耦(odd-even decoupling)(即产生两套相互独立的离散解),因此必须加入所谓人工耗散(artificial dissipation)(因其与粘性项类似)以实现稳定化。最著名的实现来自Jameson等人$^{[143]}$:在结构网格上,采用按对流通量Jacobian最大特征值缩放的二阶与四阶差分的混合;在非结构网格上则使用无分割Laplacian与双调和算子的组合$[144]$。通过对每个方程采用不同缩放因子可显著改进该格式,称为矩阵耗散格式(matrix dissipation scheme)$[145]$。需要指出的是,在非结构混合单元网格上,将显式Runge-Kutta时间推进与常规中心格式组合时可能变得不稳定$[146]$。
迎风格式
另一类是更先进的空间离散格式,它们在构造时考虑了Euler方程的物理特性。由于能够区分上游与下游影响(波传播方向),因此称为迎风格式(upwind schemes)。它们大体可分为四组:
- 通量向量分裂(flux-vector splitting)
- 通量差分分裂(flux-difference splitting)
- 总变差不增(TVD)格式(total variation diminishing)
- 波动分裂(fluctuation-splitting)格式
下面分别简要说明。
通量向量分裂格式
一类通量向量分裂格式根据某些特征变量的符号将对流通量向量分解为两部分。这些特征变量一般与对流通量Jacobian的特征值相似但不完全相同,然后对两部分分别采用迎风偏置差分离散。此类最早格式由Steger与Warming$[147]$以及Van Leer$[148]$在20世纪80年代初提出。另一类通量向量分裂格式将通量向量分为对流部分与压力(声学)部分。该思想用于Liou等人的AUSM(advection upstream splitting method)$[149,150]$,以及Jameson的CUSP(convective upwind split pressure)格式$[151,152]$。类似方法还有Edwards提出的低耗散通量分裂(LDFSS)$[153]$,以及Rossow的基于Mach数的对流-压力分裂(MAPS)$[154,155]$。第二类通量向量分裂格式近年来更受欢迎,主要因为它们对剪切层分辨更好且计算代价适中。通量向量分裂格式的另一个优点是:相较于通量差分分裂或TVD格式,它们更容易扩展到真实气体流动。我们稍后将回到真实气体模拟。
通量差分分裂格式
第二组——通量差分分裂格式——基于在界面处对不连续状态的局部一维Euler方程求解,即Riemann(激波管)问题。界面两侧通常称为左、右状态。将Riemann问题用于控制体界面的思想最早由Godunov在1959年提出$[156]$。为降低精确解Riemann问题的代价,人们发展了近似Riemann求解器,例如Osher与Solomon$[157]$以及Roe$[158]$。Roe求解器如今仍常用,因为其对边界层分辨优秀且激波表示锐利,并且可较容易地在结构网格与非结构网格上实现$[159]$。
基于Riemann问题近似求解的另一类方法称为Harten-Lax-van Leer(HLL)求解器。Einfeldt提出的变体(HLLE)$[160]$基于流体间断的稳定性理论,考虑界面处最小与最大波速;Toro等人提出的HLLC(HLL contact)$[161]$用于恢复HLL格式中的接触面,随后又被其他研究者进一步研究与修改$[162–164]$。另一个称为旋转-混合Riemann求解器的方法由Nishikawa与Kitamura提出$[165]$,旨在同时克服原始Roe格式的carbuncle现象$^{1}$以及HLL求解器在剪切层处过度耗散的问题。需要注意的是,通过对Roe格式作一个称为Harten熵修正(entropy correction)的简单修改即可容易地避免carbuncle问题。我们将在4.3.3节讨论Roe格式时给出该修改。考虑到这一点,用HLL变体替代Roe迎风格式的实际收益并不明显。
TVD格式
TVD格式的思想由Harten在1983年首次提出$[166]$。TVD格式旨在防止数值解产生新的极值。TVD格式的基本条件是:最大值不增、最小值不减,并且不生成新的局部极值。满足此性质的格式称为保持单调性(monotonicity preserving)。因此具有TVD性质的离散方法能够在无伪振荡的情况下分辨激波。TVD格式一般实现为对流通量的平均加上一个附加耗散项。耗散项可以依赖特征速度的符号,也可以不依赖;前者称为迎风TVD格式$[167]$,后者称为对称TVD格式$[168]$。经验表明,迎风TVD格式应优先采用,因为其激波与边界层分辨优于对称TVD格式。TVD格式的一个缺点是:难以方便地扩展到二阶以上的空间精度。
波动分裂格式
最后一组——波动分裂格式——提供真正的多维迎风。其目标是准确分辨那些不与网格对齐的流动结构,这相较于上述迎风格式(它们仅按网格单元取向分裂方程)是显著优势。在波动分裂方法中,流动变量与网格节点相关联;先在网格单元上以通量平衡计算中间残差(二维为三角形、三维为四面体),然后将单元残差以迎风偏置方式分配到各节点,随后用节点值更新解。
解重构
上述所有格式都需要知道控制体边界处的流动变量(如密度、速度分量或压力),可能还需分别给出界面左右两侧状态。由于我们只知道每个控制体内流动变量的平均值,因此必须进行某种插值——称为重构(reconstruction)。显然,重构的精度决定了离散格式的空间精度阶。
一阶与二阶格式
对于中心格式,将左右控制体的平均值作简单算术平均即可获得二阶精度(参见4.3.1节)。对于迎风格式,若将左右状态直接取为对应控制体的平均值,则得到一阶空间精度。要实现二阶空间精度,在结构网格上需要采用单边差分(见4.3节式(4.46));在非结构网格上实现二阶迎风格式,需先计算流动变量梯度,再用梯度与平均值通过方向导数进行左右状态插值(5.3.3节)。
ENO/WENO格式
要获得二阶以上的空间精度,可采用ENO(essentially non-oscillatory)或WENO(weighted ENO)离散方法$[177–197]$。其思想是使用不同取向的离散模板,在控制体各面构造不同的重构多项式。ENO格式选择振荡最小的多项式;WENO方法对各多项式加权组合,权重与振荡量成反比。这样在光滑区域可达到高阶精度,而在真实间断处又不会过度抹平。WENO格式的良好介绍见$[185]$。
中心格式与迎风格式的比较
一般而言,中心格式的数值代价显著更低,因此每次评估所需CPU时间也明显少于迎风格式。另一方面,迎风格式能够比中心格式更准确地捕捉间断。此外,由于数值耗散更低,迎风格式可以用更少网格点来分辨边界层。尤其是Roe的通量差分分裂格式与CUSP通量向量分裂格式能够非常精确地计算边界层。迎风格式的负面在于:当需要二阶或更高空间精度时,必须使用限制器函数(limiter functions,或简称limiters)以防止强间断附近产生伪振荡。限制器在光滑区域可能会偶然切换,从而阻碍迭代格式的收敛。Venkatakrishnan提出的一种补救方法$[198-200]$在大多数实际情形下工作良好,但仍需接受解中的小扰动。限制器的另一缺点是:计算代价较高,尤其在非结构网格上。我们将在更详细讨论迎风离散时再次回到限制器问题。
真实气体流动的迎风格式
针对真实气体模拟,特别是化学反应流动,人们提出了迎风离散格式的多种扩展。对于热力学与化学平衡的流动,Van Leer通量向量分裂$[148]$与Roe近似Riemann求解器$[158]$的修改见$[201–203]$。对于更复杂的化学与热力学非平衡流动,这两类迎风方法的表述见$[204–209]$及其中引用文献。尤其是$[203,207,208]$分别对所用方法给出了良好概述。针对化学反应流动,文献$[210]$汇总了控制方程及迎风格式可能需要的Jacobian矩阵与变换矩阵;针对平衡真实气体,类似总结见$[211]$。

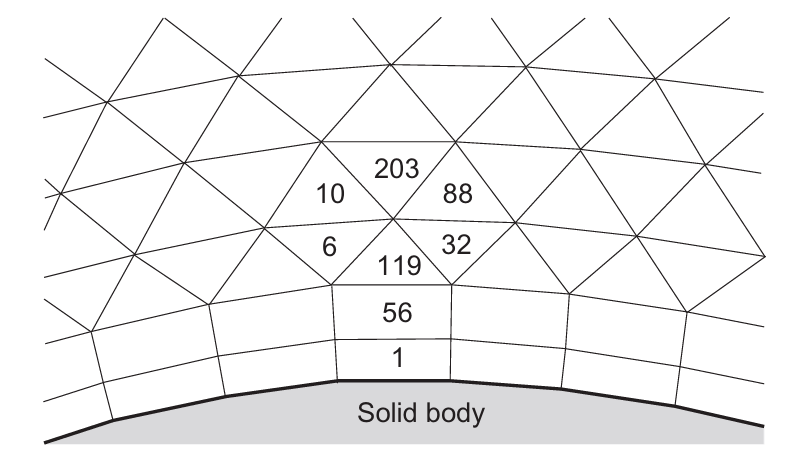 图3.3 二维非结构化混合网格方法;数字标记单个单元格。
图3.3 二维非结构化混合网格方法;数字标记单个单元格。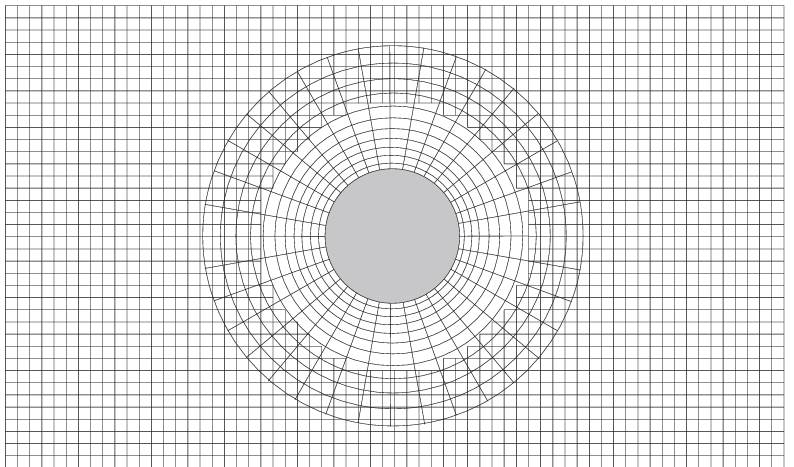 图3.5 Chimera技术示意图(二维示例)
图3.5 Chimera技术示意图(二维示例)