2.3 粘性应力

粘性应力源于流体与微元表面之间的摩擦，用应力张量$\overline{\tau}$描述。在笛卡尔坐标中，其一般形式为  

$$\overline{\overline{\tau}}=\begin{bmatrix}\tau_{xx}&\tau_{x\gamma}&\tau_{xz}\\ \tau_{\gamma x}&\tau_{\gamma\gamma}&\tau_{\gamma z}\\ \tau_{zx}&\tau_{z\gamma}&\tau_{zz}\end{bmatrix}.\tag{2.14}$$  

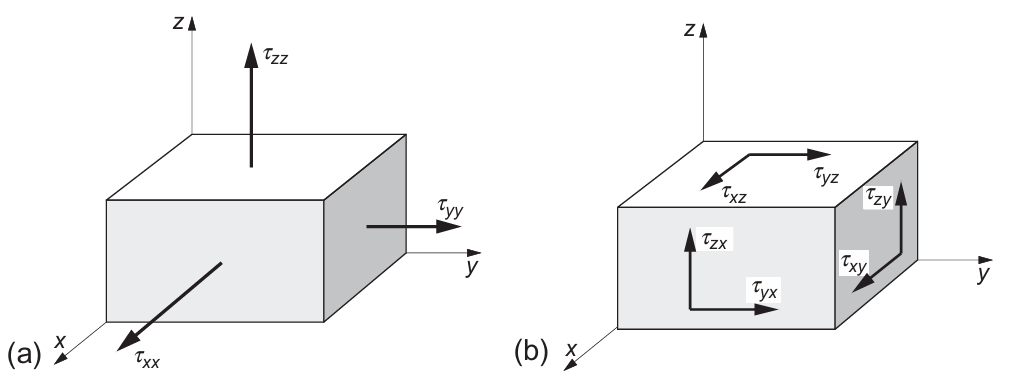
按惯例，$\tau_{ij}$表示该应力分量作用于垂直于$i$轴的平面，并沿$j$轴方向作用。$\tau_{xx}$、$\tau_{yy}$与$\tau_{zz}$为法向应力，$\overline{\tau}$的其他分量分别为剪切应力。图2.3展示了四边形流体微元上的应力。可以看到，法向应力（图2.3a）试图沿三个相互垂直方向推动微元各面发生位移，而剪切应力（图2.3b）则试图使微元发生剪切变形。

接下来问题是，如何计算粘性应力？首先，它们依赖于介质的动力学性质。对于空气或水等流体，牛顿指出剪切应力与速度梯度成正比，因此这类介质称为牛顿流体。另一方面，例如熔融塑料或血液等流体表现不同——它们属于非牛顿流体。对绝大多数实际问题，流体可视为牛顿流体，此时粘性应力张量的分量由关系式$此时粘性应力张量的分量由关系式给出$[3,4]$给出  

$$\begin{aligned}\tau_{xx}&=\lambda\left(\frac{\partial u}{\partial x}+\frac{\partial\nu}{\partial\gamma}+\frac{\partial w}{\partial z}\right)+2\mu\frac{\partial u}{\partial x},\ \tau_{\gamma\gamma}=\lambda\left(\frac{\partial u}{\partial x}+\frac{\partial\nu}{\partial\gamma}+\frac{\partial w}{\partial z}\right)+2\mu\frac{\partial\nu}{\partial\gamma},\ \tau_{zz}=\lambda\left(\frac{\partial u}{\partial x}+\frac{\partial\nu}{\partial\gamma}+\frac{\partial w}{\partial z}\right)+2\mu\frac{\partial w}{\partial z},\ \tau_{x\gamma}=\tau_{\gamma x}=\mu\left(\frac{\partial u}{\partial\gamma}+\frac{\partial\nu}{\partial x}\right),\ \tau_{xz}=\tau_{zx}=\mu\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right),\ \tau_{\gamma z}=\tau_{z\gamma}=\mu\left(\frac{\partial\nu}{\partial z}+\frac{\partial w}{\partial\gamma}\right)\end{aligned}\tag{2.15}$$  

其中$\lambda$为第二粘度系数，$\mu$为动力粘度系数。为方便起见，还可定义运动粘度系数  

$$\nu=\mu/\rho.\tag{2.16}$$  

式(2.15)由英国人George Stokes在19世纪中期推导得到。法向应力中的$\mu(\partial u/\partial x)$等项代表线性胀缩率（形状变化）。另一方面，式(2.15)中的$(\lambda\,\mathrm{div}\,\vec{v})$项代表体积胀缩率——体积变化率，本质上对应密度的变化。

为封闭法向应力表达式，Stokes提出假设$[5]$  

$$\lambda+\frac{2}{3}\mu=0.\tag{2.17}$$  

上述关系式(2.17)称为体粘度（bulk viscosity）。体粘度表征的是：在温度均匀的流体中，当体积以有限速率变化时导致能量耗散的性质。

除极高温或极高压之外，目前尚无实验证据表明式(2.17)中的Stokes假设不成立（见文献$[6]$讨论）。因此通常用它从式(2.15)中消去$\lambda$，从而得到法向粘性应力  

$$\tau_{xx}=2\mu\left(\frac{\partial u}{\partial x}-\frac{1}{3}\mathrm{div}\,\vec{\nu}\right),$$  

$$\tau_{\gamma\gamma}=2\mu\left(\frac{\partial\nu}{\partial\gamma}-\frac{1}{3}\mathrm{div}\,\vec{\nu}\right),\tag{2.18}$$  

$$\tau_{zz}=2\mu\left(\frac{\partial w}{\partial z}-\frac{1}{3}\mathrm{div}\,\vec{\nu}\right).$$  

应注意，对于不可压缩流体（密度恒定），由于$\vec{\nu}=0$（连续方程），式(2.18)中的法向应力表达式将简化。

剩下需要确定的是：粘度系数$\mu$与导热系数$k$作为流体状态函数的形式。在连续介质力学框架下，这只能基于经验假设来完成。我们将在下一节回到这个问题。