2.2 守恒定律

      若将注意力限制在单相流体上，质量守恒定律表达的是：在流体系统中质量既不会产生，也不会消失。连续方程中也不存在扩散通量项，因为对于静止流体而言，质量的任何变化都意味着流体粒子的位移。

      为推导连续方程，考虑如图2.1所示、固定在空间中的有限控制体模型。在控制面上一点处，流速为$\vec{\nu}$，单位法向量为$\vec{n}$，$\mathrm{d}S$为微小面积元。此时守恒量为密度$\rho$。有限体积$\Omega$内总质量随时间的变化率为  

$$\frac{\partial}{\partial t}\int_{\Omega}\rho\mathrm{d}\Omega.$$  

   流体通过某一固定空间表面的质量流量等于（密度）×（面积）×（垂直于该表面的速度分量）。因此，对流通量在每个面元$\mathrm{d}S$上的贡献为  

$$\rho(\vec{\nu}\cdot\vec{n})\mathrm{d}S.$$  

由于在对流项中$\vec{n}$总是指向控制体外侧，若$(\vec{v}\cdot\vec{n})$为负则称为入流（inflow），若为正则称为出流（outflow），此时质量离开控制体。

      如上所述，不存在体源或面源。因此，考虑式(2.1)的一般表达式，可写为  

$$\frac{\partial}{\partial t}\int_{\Omega}\rho\mathrm{d}\Omega+\oint_{\partial\Omega}\rho(\vec{\nu}\cdot\vec{n})\mathrm{d}S=0.\tag{2.3}$$  

这就是连续方程（质量守恒定律）的积分形式。

      我们可以从回忆Newton第二定律的特定表述开始推导动量方程：动量的变化由作用在质量元上的合力引起。对于控制体$\Omega$内一个无穷小部分（见图2.1），其动量为  

$$\rho\vec{\nu}\mathrm{d}\Omega.$$  

控制体内动量随时间的变化为  

$$\frac{\partial}{\partial t}\int_{\Omega}\rho\vec{\nu}\mathrm{d}\Omega.$$  

因此，此处的守恒量是密度与速度的乘积，即  

$$\rho\vec{\nu}=\left[\rho u,\rho\nu,\rho w\right]^{\mathrm{T}}.$$  

      描述动量穿过控制体边界传递的对流通量张量，在笛卡尔坐标系中由以下三个分量组成  

$$\begin{aligned}&x\text{-component:}\quad\rho\vec{u\nu}\\&\gamma\text{-component:}\quad\rho\vec{v\nu}\\&z\text{-component:}\quad\rho\vec{w\nu}.\end{aligned}$$  

对流通量张量对动量守恒的贡献为  

$$-\oint_{\partial\Omega}\rho\vec{\nu}(\vec{\nu}\cdot\vec{n})\mathrm{d}S.$$  

      扩散通量为零，因为流体静止时不可能发生动量扩散。接下来的问题是：流体微元受到哪些力？我们可以识别出作用于控制体的两类力：

1. 外部体力（或质量力），它们直接作用于体积内的质量。例如重力、浮力、Coriolis力或离心力。在某些情况下，还可能存在电磁力。  

2. 面力，它们直接作用于控制体表面，仅来自以下两种来源：  

(a) 由控制体周围流体施加的压力分布；  

(b) 由流体与控制体表面摩擦产生的剪应力与法向应力。

由此可见，单位体积的体力（外力），记为$\rho\vec{f}_{e}$，对应式(2.2)中的体源。因此体力对动量守恒的贡献为  

$$\int_{\Omega}\rho\vec{f}_{e}\mathrm{d}\Omega.$$  

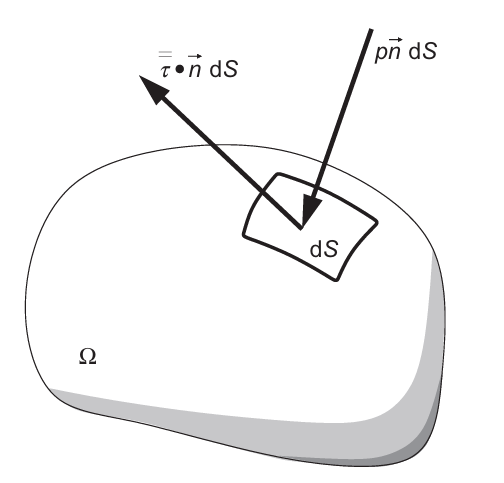
面源由两部分组成——各向同性的压力项与粘性应力张量$\overline{\overline{\tau}}$，即  

$$\overline{\overline{Q}}_{S}=-p\overline{\overline{I}}+\overline{\overline{\tau}}\tag{2.4}$$  

其中$\overline{I}$为单位张量（关于张量可参见例如[2]）。面源对控制体的作用如图2.2所示。在2.3节中，我们将更详细地讨论应力张量的形式，特别是说明法向与剪切应力如何与流速相关。

因此，将以上各项按一般守恒定律（式(2.2)）相加，最终得到  

$$\frac{\partial}{\partial t}\int_{\Omega}\rho\vec{\nu}\mathrm{d}\Omega+\oint_{\partial\Omega}\rho\vec{\nu}(\vec{\nu}\cdot\vec{n})\mathrm{d}S=\int_{\Omega}\rho\vec{f}_{e}\mathrm{d}\Omega-\oint_{\partial\Omega}p\vec{n}\mathrm{d}S+\oint_{\partial\Omega}(\overline{\overline{\tau}}\cdot\vec{n})\mathrm{d}S\tag{2.5}$$  

这就是固定在空间中的任意控制体$\Omega$内动量守恒的积分表达式。

推导能量方程所依据的原理是热力学第一定律。将其应用于图2.1所示控制体，意味着体积内总能量随时间的任何变化，均由作用于该体积的力所做功率以及进入体积的净热通量所引起。流体单位质量的总能量$E$等于单位质量内能$e$与单位质量动能$|\vec{\nu}|^{2}/2$之和。因此  

$$E=e+\frac{|\vec{\nu}|^{2}}{2}=e+\frac{u^{2}+\nu^{2}+w^{2}}{2}.\tag{2.6}$$  

此时守恒量为单位体积总能量$\rho E$。其在体积$\Omega$内随时间的变化可表示为  

$$\frac{\partial}{\partial t}\int_{\Omega}\rho E\mathrm{d}\Omega.$$  

沿着推导一般守恒定律（式(2.1)）时的讨论，我们可直接写出对流通量贡献  

$$-\oint_{\partial\Omega}\rho E(\vec{\nu}\cdot\vec{n})\mathrm{d}S.$$  

与连续方程和动量方程不同，此处存在扩散通量。如前所述，它与单位质量守恒量的梯度成正比（Fick定律）。由于扩散通量$\tilde{F}_{D}$定义于静止流体，因此只有内能项起作用，从而得到  

$$\vec{F}_{\mathrm{D}}=-\gamma\rho\kappa\nabla e,\tag{2.7}$$  

其中$\gamma=c_{p}/c_{v}$为定压与定容比热之比，$\kappa$为热扩散系数。扩散通量代表进入控制体净热通量的一部分，即由分子热传导导致的热扩散——由温度梯度引起的传热。因此，式(2.7)一般写成Fourier热传导定律形式  

$$\vec{F}_{\mathrm{D}}=-k\nabla T\tag{2.8}$$  

其中$k$为导热系数，$T$为绝对静温。

进入有限控制体的净热通量的另一部分由体积加热构成，例如辐射的吸收/发射或化学反应导致的加热。我们将热源（单位质量的热传递率）记为$\dot{q}_{h}$。它与体力$\vec{f}_{e}$（在动量方程中引入）对流体做功率一起，构成体源项  

$$Q_{V}=\rho\vec{f}_{e}\cdot\vec{\nu}+\dot{q}_{h}.\tag{2.9}$$  

尚需确定的能量守恒最后一项是面源$Q_{S}$。它对应压力以及剪切与法向应力对流体微元所做功率（见图2.2），即  

$$\vec{Q}_{S}=-p\vec{\nu}+\overline{\overline{\tau}}\cdot\vec{\nu}.\tag{2.10}$$  

整理以上各项与各项贡献，可得到能量守恒方程  

$$\begin{align*}\frac{\partial}{\partial t}\int_{\Omega}\rho E\mathrm{d}\Omega+\oint_{\partial\Omega}\rho E(\vec{\nu}\cdot\vec{n})\mathrm{d}S=&\oint_{\partial\Omega}k(\nabla T\cdot\vec{n})\mathrm{d}S+\int_{\Omega}\left(\rho\vec{f_{e}}\cdot\vec{\nu}+\dot{q}_{h}\right)\mathrm{d}\Omega-\oint_{\partial\Omega}p(\vec{\nu}\cdot\vec{n})\mathrm{d}S+\oint_{\partial\Omega}(\overline{\overline{\tau}}\cdot\vec{\nu})\cdot\vec{n}\mathrm{d}S.\end{align*}\tag{2.11}$$  

能量方程(2.11)通常写成略有不同的形式。为此，我们利用总焓、总能量与压力之间的一般关系  

$$H=h+\frac{|\vec{\nu}|^{2}}{2}=E+\frac{p}{\rho}.\tag{2.12}$$  

将能量守恒定律(2.11)中的对流项$(\rho E\vec{\nu})$与压力项$(p\vec{\nu})$合并，并应用式(2.12)，即可将能量方程写成最终形式  

$$\begin{align*}\frac{\partial}{\partial t}\int_{\Omega}\rho E\mathrm{d}\Omega+\oint_{\partial\Omega}\rho H(\vec{\nu}\cdot\vec{n})\mathrm{d}S=&\oint_{\partial\Omega}k(\nabla T\cdot\vec{n})\mathrm{d}S+\int_{\Omega}\left(\rho\vec{f_{e}}\cdot\vec{\nu}+\dot{q}_{h}\right)\mathrm{d}\Omega+\oint_{\partial\Omega}(\overline{\overline{\tau}}\cdot\vec{\nu})\cdot\vec{n}\mathrm{d}S.\end{align*}\tag{2.13}$$  

至此，我们推导出了三条守恒定律的积分形式：质量守恒(2.3)、动量守恒(2.5)以及能量守恒(2.13)。下一节将更详细地推导法向与剪切应力的表述。