2.1 流动及其数学描述
流体力学主方程的推导基于这样一个事实:流体的动力学行为由以下守恒定律所决定,即:
1. 质量守恒。
2. 动量守恒,
3. 能量守恒。
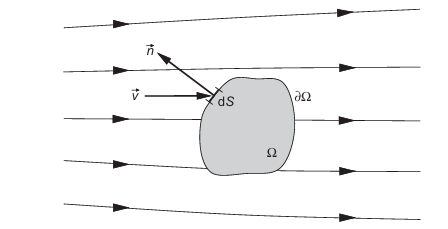
2.1.1 有限控制体
$$\frac{\partial}{\partial t}\int_{\Omega}U\mathrm{d}\Omega$$
等于如下各项贡献之和:首先是对流通量的贡献——量$U$以速度$\vec{\nu}$穿过边界进入控制体的部分,
$$-\oint_{\partial\Omega}U(\vec{\nu}\cdot\vec{n})\mathrm{d}S,$$
图2.1有限控制体积的定义(空间固定)
$$\oint_{\partial\Omega}\kappa\rho[\nabla(U/\rho)\cdot\vec{n}]\mathrm{d}S,$$
其中$\kappa$为热扩散系数;最后是体源与面源$Q_{V}$、$\vec{Q}_{S}$的贡献,即
$$\int_{\Omega}Q_{V}\mathrm{d}\Omega+\oint_{\partial\Omega}(\vec{\boldsymbol{Q}}_{S}\cdot\vec{\boldsymbol{n}})\mathrm{d}S.$$
$$\frac{\partial}{\partial t}\int_{\Omega}U\mathrm{d}\Omega+\oint_{\partial\Omega}\left[U(\vec{\nu}\cdot\vec{n})-\kappa\rho(\nabla U^{*}\cdot\vec{n})\right]\mathrm{d}S=\int_{\Omega}Q_{V}\mathrm{d}\Omega+\oint_{\partial\Omega}(\vec{Q}_{S}\cdot\vec{n})\mathrm{d}S,\tag{2.1}$$
其中$U^{*}$表示单位质量上的量$U$,即$U/\rho$。
$$\frac{\partial}{\partial t}\int_{\Omega}\vec{U}\mathrm{d}\Omega+\oint_{\partial\Omega}\left[(\overline{\overline{F}}_{\mathrm{C}}-\overline{\overline{F}}_{\mathrm{D}})\cdot\vec{n}\right]\mathrm{d}S=\int_{\Omega}\vec{Q}_{V}\mathrm{d}\Omega+\oint_{\partial\Omega}(\overline{\overline{Q}}_{S}\cdot\vec{n})\mathrm{d}S.\tag{2.2}$$
由式(2.1)或式(2.2)给出的守恒定律积分形式具有两个非常重要且令人满意的性质:
1. 若不存在体源,则$U$的变化只取决于穿过边界$\partial\Omega$的通量,而不取决于控制体$\Omega$内部的任何通量。
2. 当流场存在如激波或接触间断等不连续时,这种形式仍然有效$[1]$。